اندکی در باب نوار موبیوس

با سلام خدمت بازدیدکنندگان این وبلاگ. از وقفه ی پیش آمده عذرخواهی می کنم.

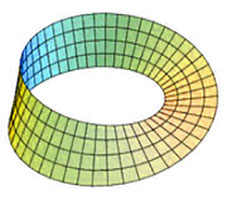
مطلبی که هم اکنون میخوانید، در مورد یک شیء بسیار جالب از دنیای ریاضیات است: نوار موبیوس.

نوار موبیوس توسط آگوست فرنیناند موبیوس و یوهان بندیکت به صورت جداگانه کشف و به ثبت رسید.

این شیء جالب، چیزی نیست جز یک نوار کاغذی! البته نواری که در طول خود، یک بار پیچ خورده است.

در ادامه، به طور شهودی این نوار را بررسی میکنیم:

 

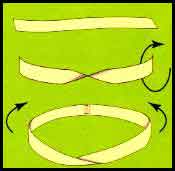
یک نوار کاغذی را بردارید و دو سر آن را به هم بچسبانید. یک حلقه ی کاغذی ساده به وجود خواهد آمد. اگر آن را از وسط نصف کنید، دو حلقه ی نازک تر به وجود خواهند آمد. اگر آن حلقه ها را نیز از وسط برش دهید، باز هم حلقه های دیگری به وجود خواهند آمد. چیز عجیب و غیر منتظره ای در اینجا وجود ندارد.

دوباره یک نوار کاغذی بردارید؛ ولی این بار، یک بار نوار را 180 درجه پیچ دهید و سپس دو سر آن را به هم بچسبانید. نتیجه، به ظاهر یک حلقه ی کاغذی پیچ خورده است؛ ولی در واقع، شما یک نوار موبیوس پیش رو دارید که خواص آن شما را متعجب خواهند کرد!

شاید به سختی باور کنید که این نوار موبیوس، پشت ندارد!! بله، نوار موبیوس تنها یک رو دارد و اگر این را باور ندارید، میتوانید امتحان کنید. نواری که در بالا ساختید را بردارید و از وسط آن با مداد، خطی رسم کنید. اگر این خط را ادامه دهید، تا جایی که به نقطه ی شروع برسید، خواهید دید که خط در هر دو سمت کاغذ رسم شده است!  نه یک طرف آن!

شکل زیر، میتواند به درک این موضوع کمک کند:

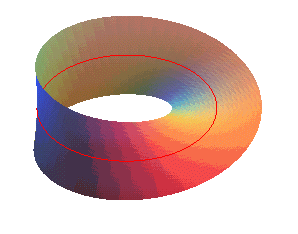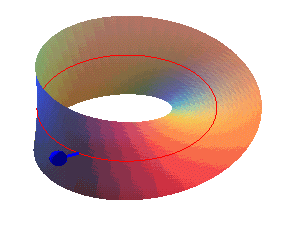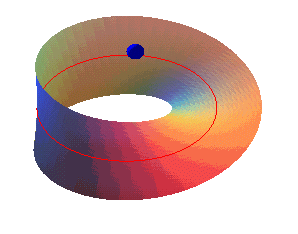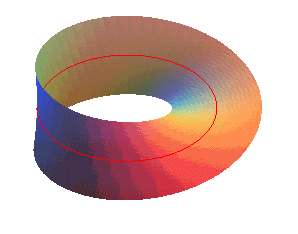
در واقع،  شما در نقطه ای از آن ایستاده باشید و بخواهید به همان نقطه در سمت دیگر کاغذ برسید، لازم نیست از لبه های کاغذ عبور کنید و تنها با قدم زدن، به نقطه ی مقصد خواهید رسید!

حال به شگفتی دیگری از این نوار می پردازیم. به نظر شما، اگر این نوار را از وسط برش دهیم، نتیجه ی کار چه خواهد بود؟ دو حلقه؟

ولی باید بگویم که اینطور نیست و حاصل، یک حلقه ی بزرگتر خواهد بود که دو بار در طول خود پیچ خورده است! میتوانید به صورت عملی هم ببینید.

حال یک سوال دیگر می پرسم: اگر همین حلقه ی بزرگ را دوباره از وسط برش دهیم، این بار نتیجه چه خواهد بود؟ یک حلقه ی بزرگتر با سه بار پیچ خوردن؟ یا چهار بار پیچ خوردن؟

این بار هم پاسخ، اشتباه بود. در کمال شگفتی، این دفعه حاصل دو حلقه خواهد بود که در هم تنیده اند! جالبتر اینکه یکی از این حلقه ها نوار موبیوس است؛ ولی حلقه دیگر که چندبار پیچ خورده است، نوار موبیوس نیست. 

با برش دادن این حلقه ها، حتما به نتایج جالبی دست خواهید یافت.

حال یک نوار موبیوس دیگر بسازید و به صورت طولی برش دهید؛ اما نه از وسط، بلکه از یک سوم عرض آن. این کار را ادامه دهید تا به نقطه شروع برش برسید. این بار نتیجه شما را متعجب خواهد کرد. چون به جای همان حلقه ی بلند، دو نوار موبیوس در اندازه های مختلف خواهید داشت!!.

خب، امیدوارم از این مطلب لذت برده باشید و به دانسته هایتان افزوده شده باشد.

و همچنین فهمیده باشید که نیم دور پیچ خوردن چطور میتواندباعث این همه شگفتی شود!!