درباره ی نسبت طلایی، نشانه ای زیبا و اعجاب انگیز از ریاضیات

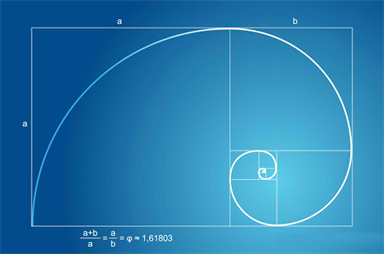
دو پاره خط با اندازه های متفاوت را در نظر بگیرید؛ به طوریکه نسبت طول پاره خط بزرگتر به کوچکتر، برابر با نسبت مجموع طول پاره خط ها بر طول پاره خط بزرگتر باشد. مقدار این دو نسبت، همواره مقداری ثابت و یک عدد گنگ خواهد بود که آن را نسبت طلایی نامیده اند. رابطه زیر این موضوع را به زیان ریاضی نشان می دهد:

نسبت طلایی را با حرف  Φ (فی) یونانی نیز نشان می دهند. بنا به تعبیری، این حرف همان حرف نخست از نام فیدیاس، (Φειδίας) پیکرتراش مشهور یونانی می باشد که در آثار خود به وفور از این نسبت استفاده می کرده است. (انسان از دیرباز متوجه این عدد بوده و از آن بهره می برده است.) 

 

مقدار نسبت طلایی

رابطه ی زیر را مجدد در نظر بگیرید:

اگر در نظر بگیریم که  ، طبق محاسبات زیر به رابطه  می رسیم:

یا به عبارتی:

از این معادله به یک معادله درجه دو به صورت زیر می رسیم:

این معادله دو جواب دارد: 

از آنجایی که نسبت دو مقدار مثبت نمی تواند منفی باشد، بنابراین جواب دوم منتفی است و مورد اول  مقبول می باشد.

این جواب یک عدد گنگ خواهد بود، تقریبا برابر با:

ناگفته نماند که نسبت طلایی را می توان به صورت یک کسر مسلسلی هم نوشت:

نسبت طلایی و اعداد فیبوناتچی

دنباله ی فیبوناتچی، رشته ای از اعداد است که در آن، هر جمله برابر با مجموع دو جمله ی قبل از خود می باشد.

شکل معروف آن، که دو جمله ی اول آن هر دو 1 هستند، به صورت زیر است:

«1, 1, 2, 3, 5, 8, 13, 21, ...»

جملات دنباله فیبوناتچی، رابطه ی تنگاتنگی با نسبت طلایی دارند. نمونه ای از تجلی آن را در این مطلب بررسی میکنیم:

دوجمله ی متوالی از این دنباله را در نظر بگیرید و نسبت جمله ی بزرگتر به کوچکتر را حساب کنید. جدول زیر این محاسبه را برای تعدادی از جملات نشان می دهد:

جمله اول	جمله دوم	نسبت جمله دوم به اول
1	1	1
1	2	2
2	3	1.5
3	5	1.67
5	8	1.6

به همین ترتیب، مقدار ردیف سوم به تدریج به مقدار نسبت طلایی نزدیک تر می شود یا به عبارتی «میل می کند».

***

مربع هایی را در نظر بگیرید که طول ضلع هر کدام برابر با یکی از جملات دنباله فیبوناتچی باشد. سپس این مربع ها را به مانند تصویر زیر در کنار هم قرار دهید:

اگر قطر های هر یک از مربع ها را رسم کنیم، به شکلی مارپیچ مانند می رسیم که به آن مارپیچ فیبوناتچی گفته می شود (در تصویر زیر، برای ملموس تر شدن شکل مارپیچ، کمان هایی مناسب به جای قطر ها ترسیم شده اند.)

با توجه به اینکه طول اضلاع مربع ها همان جملات دنباله فیبوناتچی هستند و نسبت جملات این دنباله با یکدیگر برابر با نسبت طلایی است، میتوان گفت که این مارپیچ نسبت طلایی را هم در بر میگیرد.

نسبت طلایی در طبیعت

جلوه های بی شماری از نسبت طلایی را می توان در طبیعت یافت. به عنوان مثال، ابعاد استخوان های بدن انسان تقریبا دارای این نسبت با یکدیگر هستند. همچنین نسبت طلایی به نحوی عجیب برای چشم انسان خوشایند و زیباست؛ به طوریکه یکی از ترفند های ترکیب بندی در هنر های تجسمی برای جلب توجه به سوژه، استفاده از همین نسبت طلایی و مارپیچ فیبوناتچی (که در بالا ذکر شد) می باشد.

علاوه بر اینها، مارپیچ فیبوناتچی نیز به وفور در طبیعت و مناظر مختلف مشاهده می شود که هر یک از آنها، همچنین جلوه ای از نسبت طلایی در طبیعت هستند:

منبع:  ویکی پدیا

$$
{\displaystyle {\tfrac {b}{a}}={\tfrac {1}{\phi }}}